Regularization
Curse of dimensionality
in circumstances of p >> n
using all the features to predict response variable
will face two drawbacks in terms of …
- interpretability
- increase of variance (overfitting)
so, we do
feature selection
- subset selection
- shrinkage (regularization)
- dimension reduction
Subset selection
가능한 경우의 수: \(2^p\)
stepwise selection: forward, backward
Shrinkage
Ridge regression Lasso regression Elastic-net regression
아래 식을 최소로 하는 \(\beta\) 를 추정 (note: shrinkage penalty)
ridge regresssion
\[RSS + \lambda \sum_{j=1}^{p} \beta^2_j\]
\(\lambda\): tuning parameter
lasso regression
\[RSS + \lambda \sum_{j=1}^{p} |\beta_j|\]
library(glmnet)## Loading required package: Matrix## Loading required package: foreach## Loaded glmnet 2.0-16x = model.matrix(Salary~., Hitters)[,-1] # create a matrix, convert factors to a set of dummy variables
y = Hitters$Salarygrid = 10^seq(10, -2, length = 100) # lambda 를 10^10 에서 10^-2 까지 값을 갖도록 설정 ridge.mod = glmnet(x,y,alpha = 0, lambda = grid) # alpha = 0 for ridge regression, alpha = 1 for lasso regression
?glmnet # standardize = TRUE plot(ridge.mod)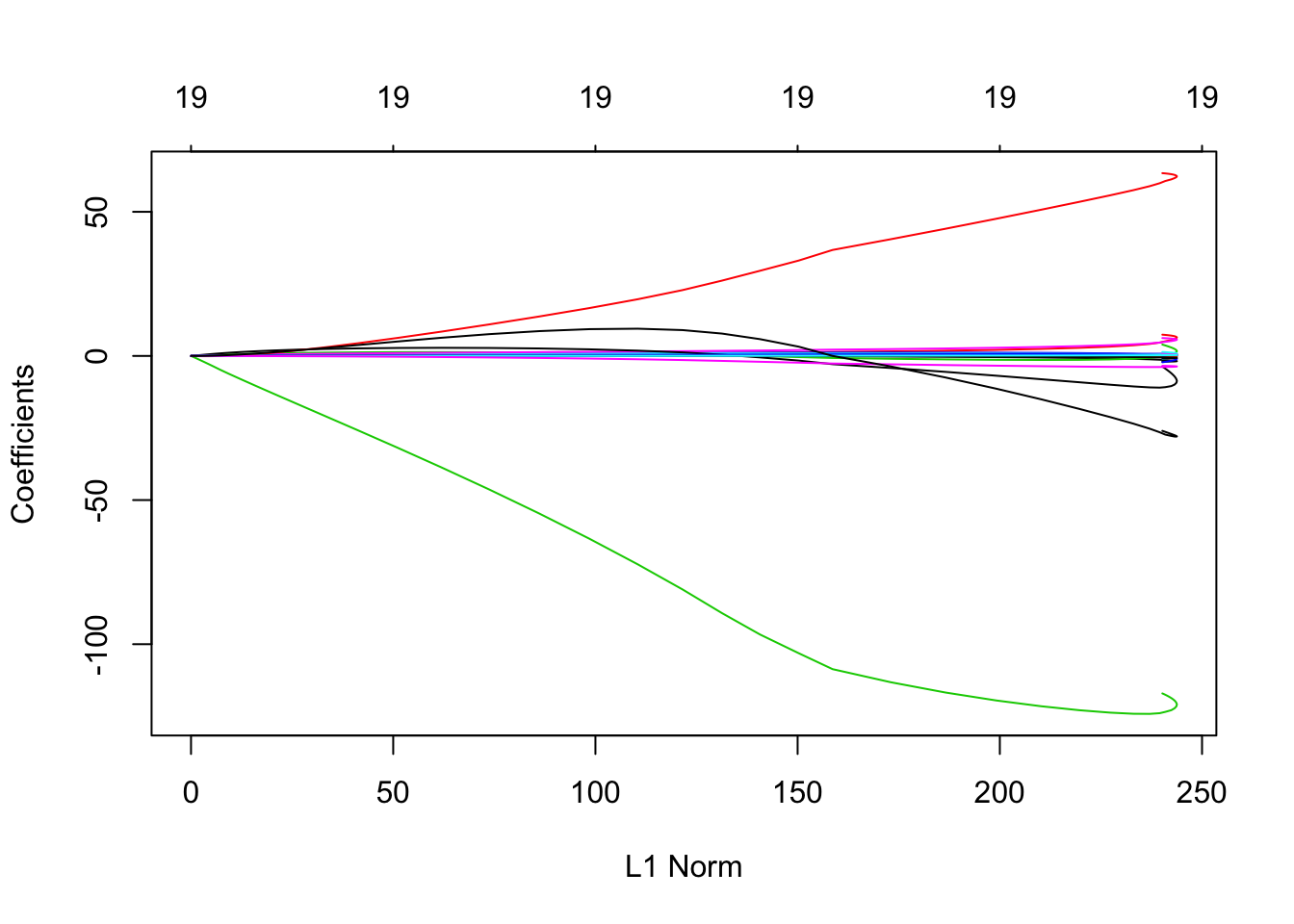
L2 norm: \(\sqrt{\sum_{j=1}^{p}\beta^2_j}\)
coef(ridge.mod)ridge.mod$lambdaridge.mod$lambda[50]## [1] 11497.57coef.50lambda = coef(ridge.mod)[-1,50] # at 50th lambda, coefficients
sqrt(sum(coef.50lambda^2)) # L2 norm at 50th lambda ## [1] 6.360612set.seed(1)
train = sample(nrow(x), nrow(x)/2)
y.test = y[-train]arbitrary set lamda = 4
ridge.mod = glmnet(x[train,], y[train], alpha = 0, lambda = grid)
ridge.pred = predict(ridge.mod, s=4, newx = x[-train,])
mean((ridge.pred-y.test)^2)## [1] 101186.3cv 를 통해 검정오차 추정치가 가장 낮은 lambda 값을 구함
set.seed(1)
cv.out.ridge = cv.glmnet(x[train,], y[train], alpha = 0) # nfolds = 10
plot(cv.out.ridge)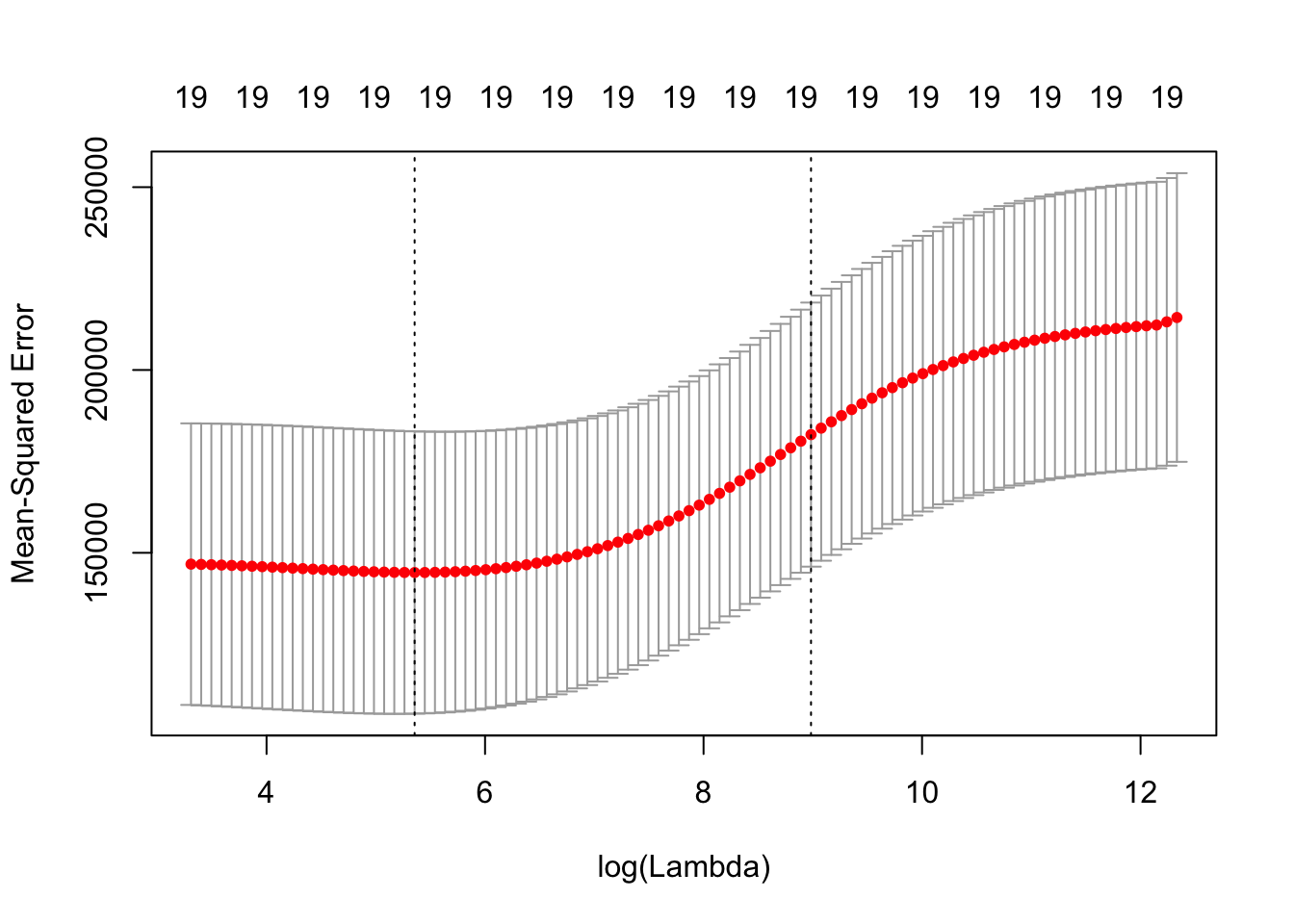
bestlambda.ridge = cv.out.ridge$lambda.min
bestlambda.ridge## [1] 211.7416cv 검정오차 추정치가 가장 낮은 lambda 값을 이용하여 검정셋에서 검정오차를 구함
ridge.pred = predict(ridge.mod, s=bestlambda.ridge, newx = x[-train,])
mean((ridge.pred - y.test)^2)## [1] 96012.47전체 데이터셋에서 ridge regression 모델을 만들고, 해당 coefficients 값을 구함
ridge.out = glmnet(x,y,alpha = 0)
predict(ridge.out, type = "coefficients", s=bestlambda.ridge)## 20 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 9.88487157
## AtBat 0.03143991
## Hits 1.00882875
## HmRun 0.13927624
## Runs 1.11320781
## RBI 0.87318990
## Walks 1.80410229
## Years 0.13074383
## CAtBat 0.01113978
## CHits 0.06489843
## CHmRun 0.45158546
## CRuns 0.12900049
## CRBI 0.13737712
## CWalks 0.02908572
## LeagueN 27.18227527
## DivisionW -91.63411282
## PutOuts 0.19149252
## Assists 0.04254536
## Errors -1.81244470
## NewLeagueN 7.21208394lasso
lasso.mod = glmnet(x[train,], y[train], alpha = 1, lambda = grid)
plot(lasso.mod)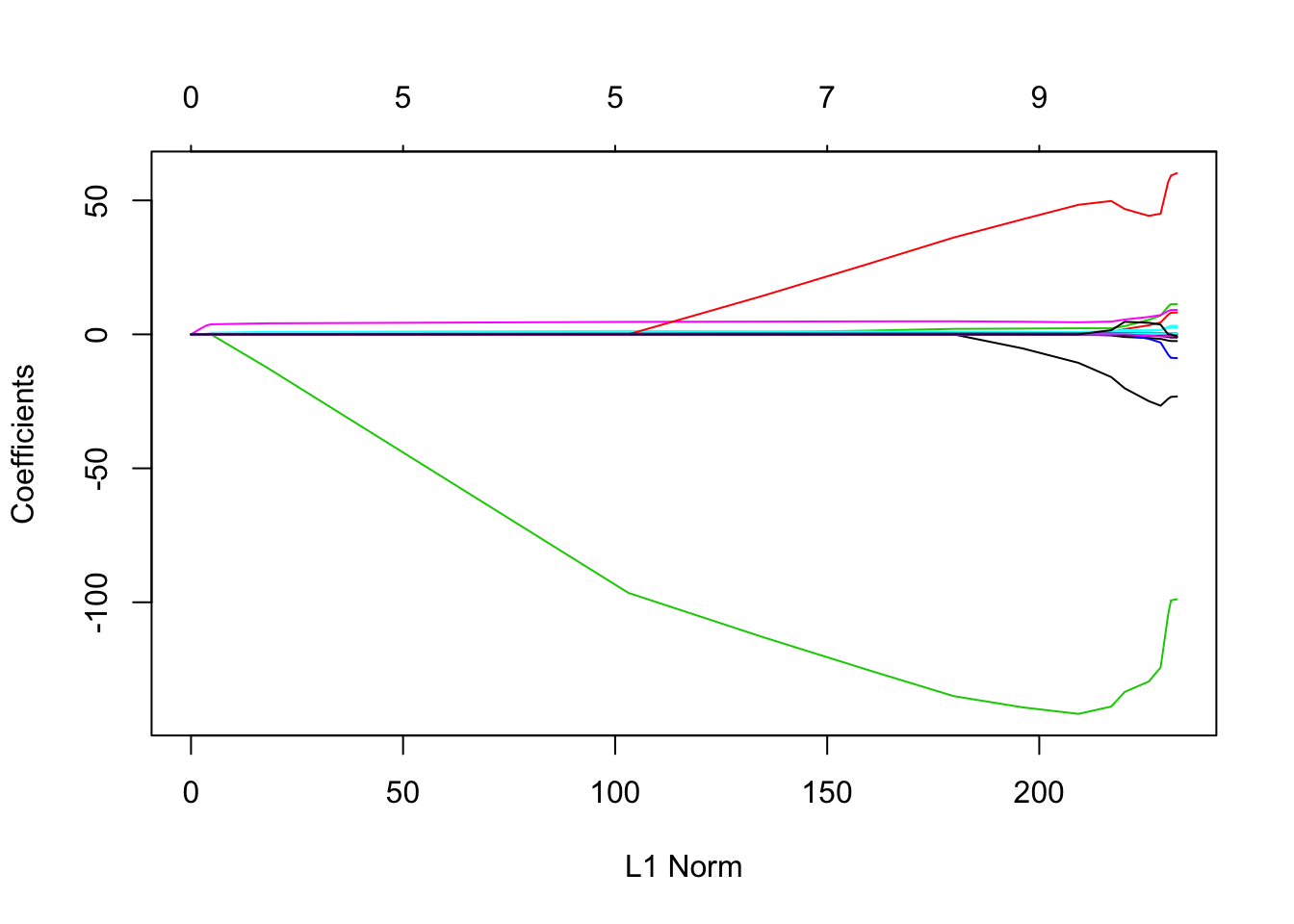
set.seed(1)
cv.lasso.out = cv.glmnet(x[train,], y[train], alpha=1)
plot(cv.lasso.out)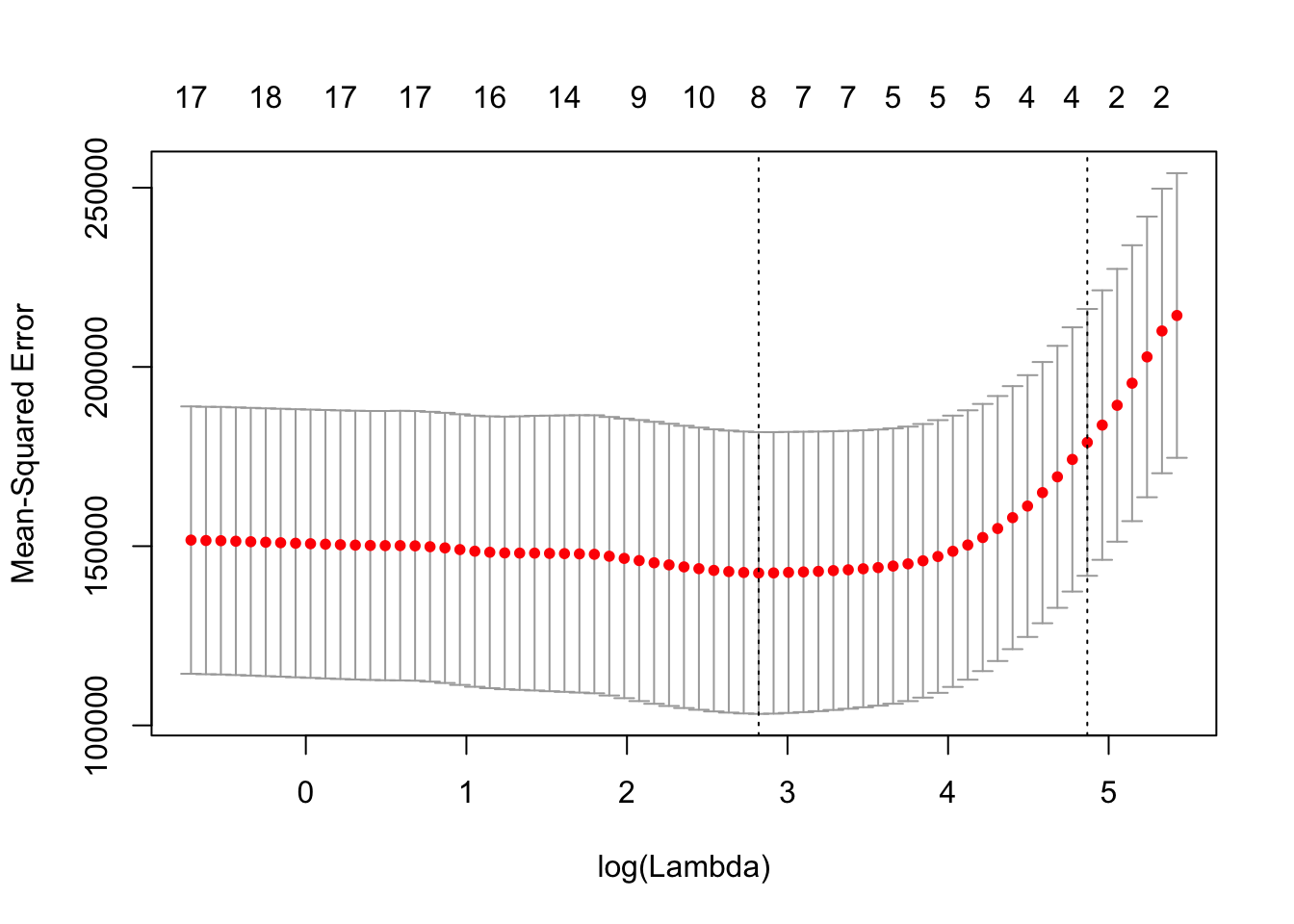
bestlambda.lasso = cv.lasso.out$lambda.min
lasso.pred = predict(lasso.mod, s=bestlambda.lasso, newx = x[-train,])
mean((lasso.pred - y.test)^2)## [1] 100743.4lasso.out = glmnet(x,y,alpha = 1, lambda = grid)
lasso.coef = predict(lasso.out, type = "coefficients", s=bestlambda.lasso)
lasso.coef## 20 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 18.5394844
## AtBat .
## Hits 1.8735390
## HmRun .
## Runs .
## RBI .
## Walks 2.2178444
## Years .
## CAtBat .
## CHits .
## CHmRun .
## CRuns 0.2071252
## CRBI 0.4130132
## CWalks .
## LeagueN 3.2666677
## DivisionW -103.4845458
## PutOuts 0.2204284
## Assists .
## Errors .
## NewLeagueN .linear regression
lm.fit = lm(Salary~., data = Hitters, subset = train)
lm.pred = predict(lm.fit, newdata = Hitters[-train,])
mean((lm.pred - y.test)^2)## [1] 114780.6Dimension reduction
- principal component regression (PCR)
- partial least square (PLS)
p개의 설명변수들을 m개의 (m
: 분산이 가장 큰 방향 (첫번째 주성분)
- PLS
- PCA의 supervised version
- 반응변수와 극대화된 상관관계를 갖도록 선형결합
library(pls)##
## Attaching package: 'pls'## The following object is masked from 'package:stats':
##
## loadingsset.seed(2)
pcr.fit = pcr(Salary~., data = Hitters, subset = train, scale = TRUE, validation = "CV")
summary(pcr.fit)## Data: X dimension: 131 19
## Y dimension: 131 1
## Fit method: svdpc
## Number of components considered: 19
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
## CV 464.6 399.3 400.5 402.3 407.0 396.6 397.6
## adjCV 464.6 398.8 399.6 401.2 405.4 395.9 394.4
## 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## CV 395.3 396.3 400.1 413.3 413.9 417.0 416.9
## adjCV 393.3 394.0 397.6 410.2 410.7 413.7 413.2
## 14 comps 15 comps 16 comps 17 comps 18 comps 19 comps
## CV 413.1 414.6 414 402.3 396.8 399.2
## adjCV 409.4 410.9 410 398.3 392.7 395.0
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
## X 38.89 60.25 70.85 79.06 84.01 88.51 92.61
## Salary 28.44 31.33 32.53 33.69 36.64 40.28 40.41
## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
## X 95.20 96.78 97.63 98.27 98.89 99.27 99.56
## Salary 41.07 41.25 41.27 41.41 41.44 43.20 44.24
## 15 comps 16 comps 17 comps 18 comps 19 comps
## X 99.78 99.91 99.97 100.00 100.00
## Salary 44.30 45.50 49.66 51.13 51.18validationplot(pcr.fit, val.type = "MSEP")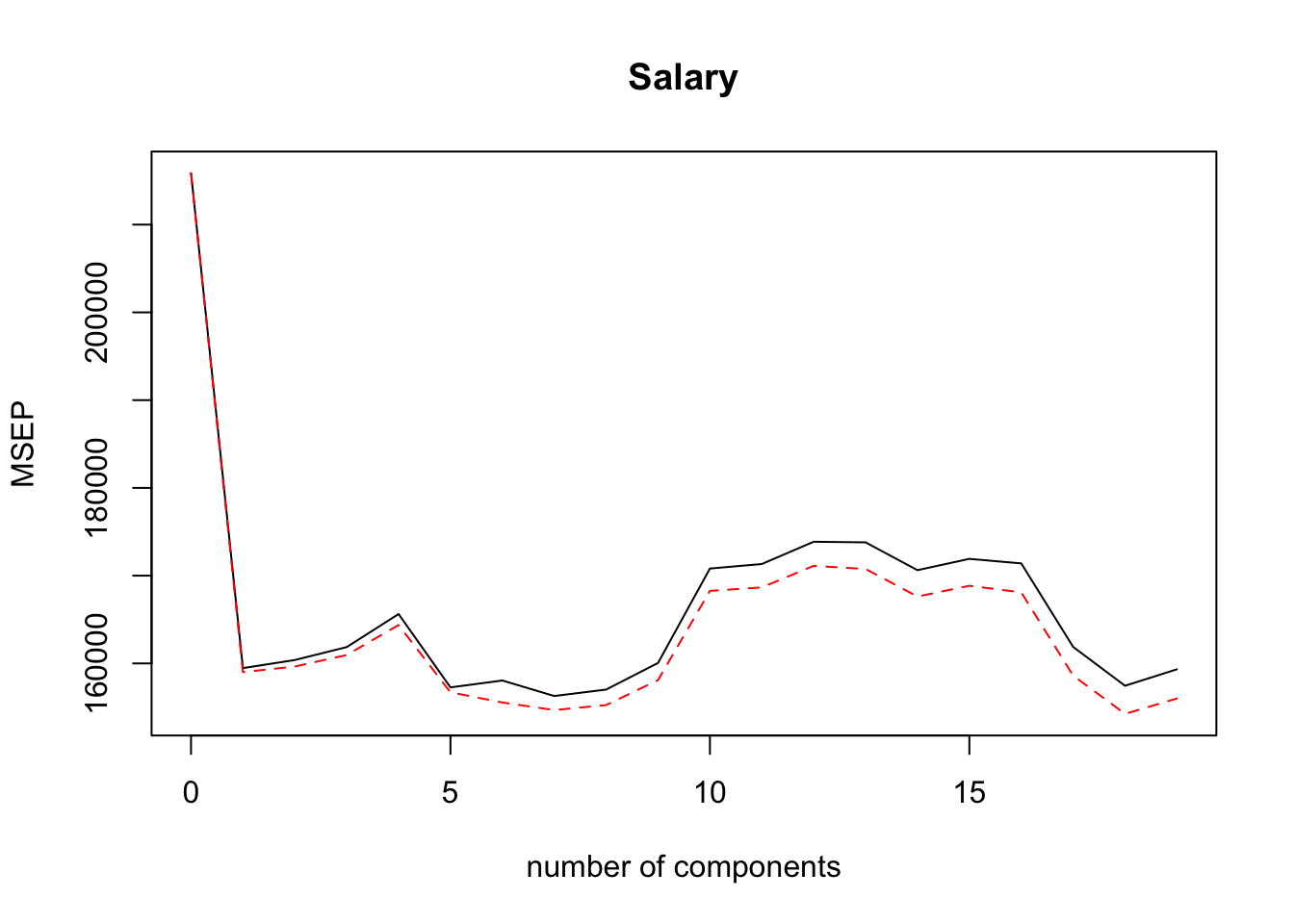
pcr.pred = predict(pcr.fit, x[-train,], ncomp = 2)
mean((pcr.pred - y.test)^2)## [1] 97563.65pcr.fit = pcr(y~x, scale = TRUE, ncomp = 2)
summary(pcr.fit)## Data: X dimension: 263 19
## Y dimension: 263 1
## Fit method: svdpc
## Number of components considered: 2
## TRAINING: % variance explained
## 1 comps 2 comps
## X 38.31 60.16
## y 40.63 41.58PLS
set.seed(1)
pls.fit = plsr(Salary~., data = Hitters, subset = train, scale = TRUE, validation = "CV")
summary(pls.fit)## Data: X dimension: 131 19
## Y dimension: 131 1
## Fit method: kernelpls
## Number of components considered: 19
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
## CV 464.6 394.2 391.5 393.1 395.0 415.0 424.0
## adjCV 464.6 393.4 390.2 391.1 392.9 411.5 418.8
## 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## CV 424.5 415.8 404.6 407.1 412.0 414.4 410.3
## adjCV 418.9 411.4 400.7 402.2 407.2 409.3 405.6
## 14 comps 15 comps 16 comps 17 comps 18 comps 19 comps
## CV 406.2 408.6 410.5 408.8 407.8 410.2
## adjCV 401.8 403.9 405.6 404.1 403.2 405.5
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
## X 38.12 53.46 66.05 74.49 79.33 84.56 87.09
## Salary 33.58 38.96 41.57 42.43 44.04 45.59 47.05
## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
## X 90.74 92.55 93.94 97.23 97.88 98.35 98.85
## Salary 47.53 48.42 49.68 50.04 50.54 50.78 50.92
## 15 comps 16 comps 17 comps 18 comps 19 comps
## X 99.11 99.43 99.78 99.99 100.00
## Salary 51.04 51.11 51.15 51.16 51.18validationplot(pls.fit, val.type = "MSEP")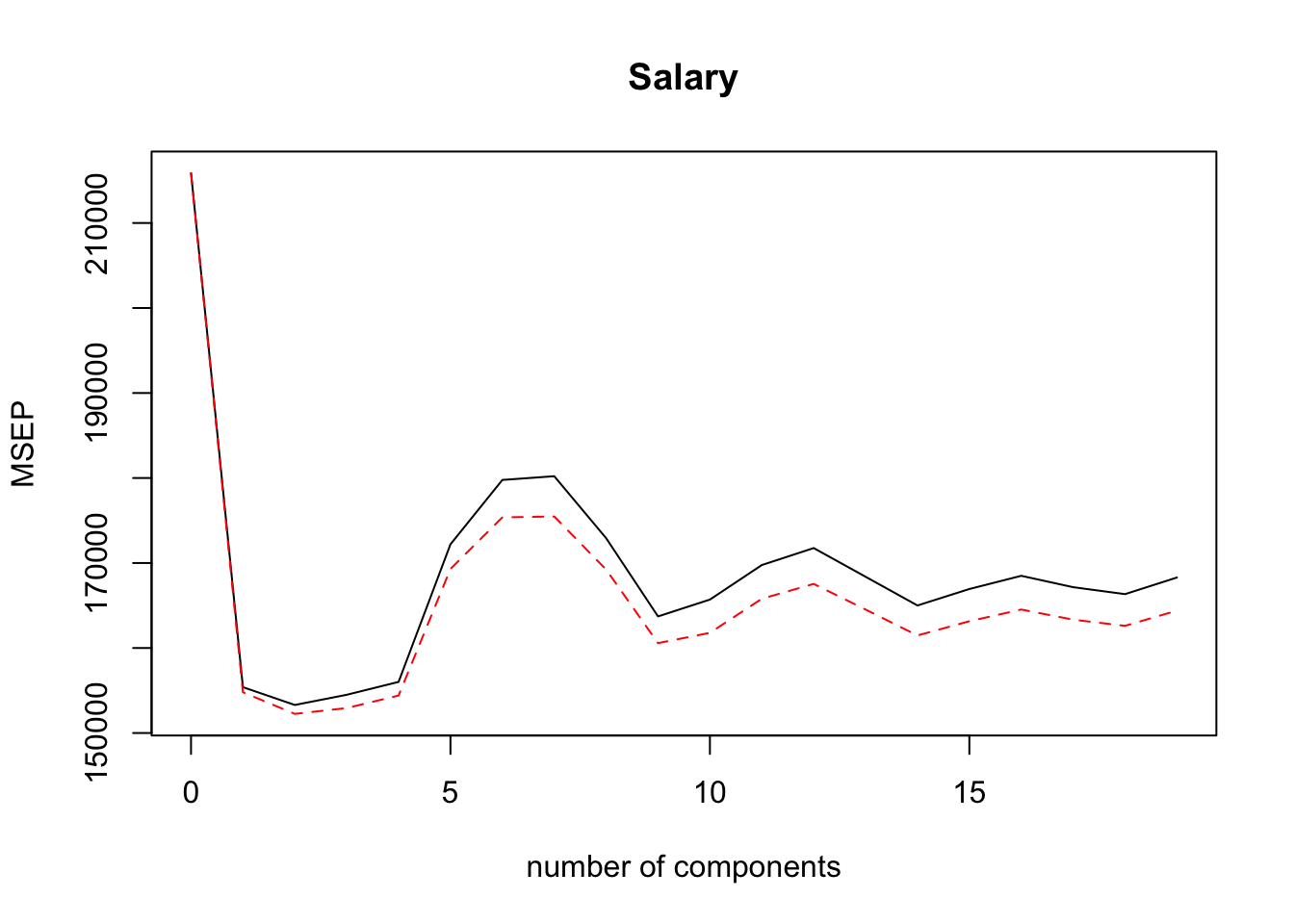
pls.pred = predict(pls.fit, x[-train,], ncomp = 2)
mean((pls.pred-y.test)^2)## [1] 101417.5pls.fit=plsr(Salary~., data=Hitters, scale=TRUE, ncomp=2)
summary(pls.fit)## Data: X dimension: 263 19
## Y dimension: 263 1
## Fit method: kernelpls
## Number of components considered: 2
## TRAINING: % variance explained
## 1 comps 2 comps
## X 38.08 51.03
## Salary 43.05 46.40